一 关于AVL树,红黑树和B树的对比
AVL树是比较原始的一个平衡树,它通过保证每个节点的两个子树的高度最多为1,来保证整棵树没有过于突出的树枝.在查找每个关键字的时候都不会有过慢的情况发生.它查找的时间复杂度是对数级的,可以实现较快的查找.
红黑树又叫做RB树,它也通过一些限制保证树的大致平衡.红黑树节点分为红色和黑色两类,红黑树要求根节点和叶子节点都必须为黑色节点,而且要求从根节点到每个叶子节点的路径上的黑色节点个数都是一样的,而且红色节点的子节点必须为黑色节点.通过着一系列的要求,就可以实现从根节点到某个叶子节点的长度不可能比到另一个叶子节点的长度的两倍还多,也就保证了整个树的大致稳定.红黑树给节点赋予了颜色,在插入或者删除节点的时候就不仅可以通过旋转,也可以通过改变颜色来保持树的平衡,这样就使得红黑树旋转的次数相对AVL树要少一些.但是红黑树因为要判断颜色,所以在操作上比AVL树要繁琐一些,所以感觉上他们在整体效率上差距并不是特别明显.通过我查阅的一些资料,发现确实是这样.红黑树现在应用非常的广泛,STL中就大量使用红黑树作为底层的实现.
B树主要广泛应用于外设存储.AVL树和红黑树虽然查找速度很快,但因受限于每个节点只能有两个节点,当数据量上去的时候,查找起来就要从根节点向下找很多层.因内存速度较快,所以对数级的时间复杂度已经可以接受了,但是在磁盘中每向下搜索一层或几层就要从磁盘中读取,对于磁盘来说这个开销是非常大的.B树的出现正是由于这个背景,它虽然在其他方面可能较AVL和红黑树差一些,但是它可以很有效的减少磁盘读取的次数,因此得到了广泛的应用.
二 B树的限制条件
- 设B树的度为m,则除了根节点外每个节点最少有m-1个关键字,最多有2m-1个关键字
- 每个节点中关键字按照非降序存放
- 每个关键字对其子树的关键字加以分割
- 每个叶子节点具有相同的深度
下图为一个度为3的B树举例
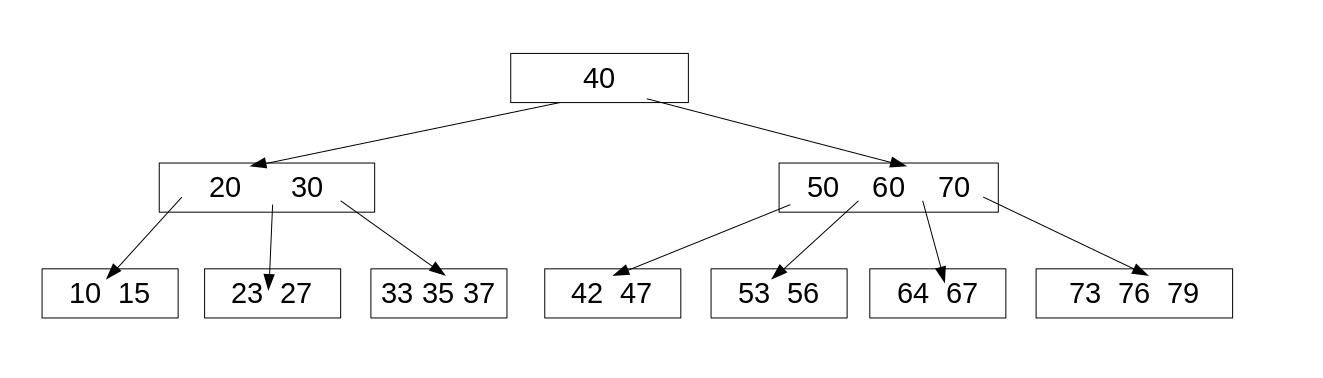
一个树的性能主要由他的插入删除操作来决定的.
三 B树的插入
- B树普通插入和红黑树插入类似,从根部一直比到叶子节点,找到想要插入的节点,如果节点没有满的话,就插入到合适位置,插入结束.
- 如果节点数量满了的话,把中间值找出来,升入父节点,原节点拆分为两个节点,如果父节点未超过最大个数,插入结束.
- 如果父节点插入后超过最大个数,则对父节点执行第二步,直至插入结束.
四 B树的删除
定义一个节点个数为m-1个时,称这个节点不丰满,否则定义为丰满.
- 搜索要删除的节点,搜索过程中,对路径上经过的节点进行判断,如果丰满则继续,如果不丰满
- 判断其兄弟节点是否丰满,如果有丰满的,则兄弟节点把合适的节点传递给父节点,父节点再把合适的节点传递给当前节点,即完成了当前节点的丰满化.
- 如果兄弟节点中没有丰满的,则选择其中一个兄弟节点,把他们父节点相应的关键字拉下来,和他们合并成一个新节点,也完成了节点的丰满化.
- 对关键字所在的节点也要进行丰满化,之后删除找到的节点,删除完成.
整个过程为我在读过了很多博客之后总结出来的算法,自己感觉比较简洁,如果有问题的话,欢迎指正.